Mumbai Indians v Chennai Super Kings on September 19, 2020 at Zayed Cricket Stadium, Abu Dhabi

A complementary scorecard

This is the first post in a series in which I describe a T20 match in a way which complements the information in the traditional scorecard. The first and second innings are treated different.

First Innings:

In the first innings, the runs expected from any delivery depend on two factors - the number of wickets in hand, and the number of legal deliveries remaining. The average expected runs from any delivery is given by the average of the runs scored from deliveries in previously completed matches (of which there are 6274 in my database at present) on which the same number of wickets were in hand, and the same number of deliveries were remaining. I use the grouping (over in match, wickets in hand, legal deliveries remaining) to estimate expected scores.

For example, in the 4th over of a T20 first innings, with 101 balls remaining and 10 wickets in hand, the expected runs from that delivery is 1.396. With 9 wickets in hand it is 1.214, while with 8 wickets in hand it is 0.876. In the 14th over of a T20 first innings, with 40 legal deliveries remaining, the expected score with 10 wickets in hand is 1.039, with 9 wickets in hand is 1.563, with 8 wickets in hand 1.351.

The Expected Score from an innings is the sum of the expected runs from each ball. The expected scores depends on when a team loses wickets. In the first innings, these expected scores can be expected to be less than the actual score at least half the time.

Second Innings:

In the second innings, the expected runs from each delivery is simply the required runs. The total expected runs is the sum of the required runs from each ball. This has some interesting implications.

For example, consider a case where 4 runs are required from 4 balls. Suppose that the 4 balls produce 1,1,1,1. In such as case, the required runs from the 4th ball is given by 4/4, from the 3rd ball by 3/3 and so on. The Required Runs in this case will be 1+1+1+1 = 4. Suppose that the 4 balls produce 0,0,2,2. In this case, the Required Runs will be given by 4/4 + 4/3 + 4/2 + 2/1 = 6.33. If the 4 balls produce 0,0,4, then the Required Runs will be 4.33.

The Required Runs provide a measure of what a chase effectively was.

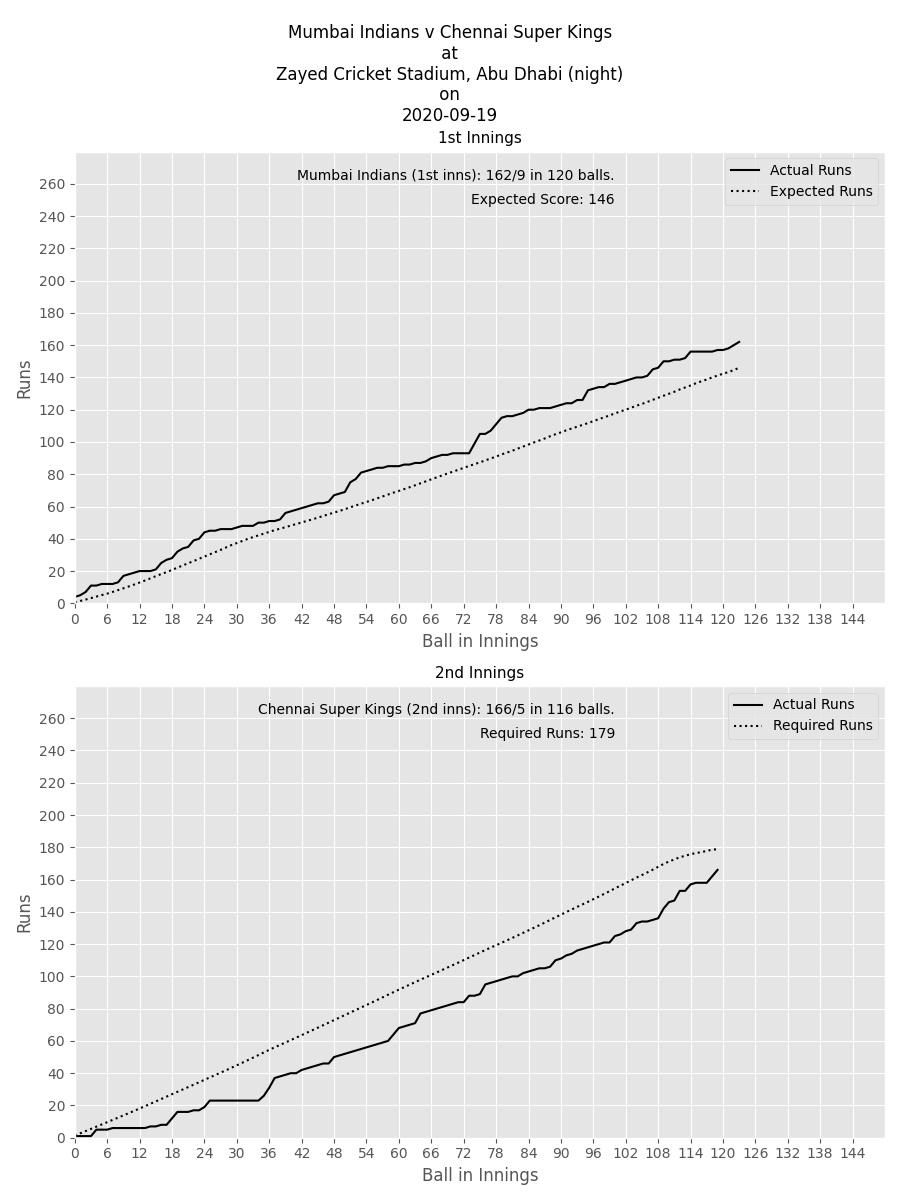
In the first match of the 2020 IPL between Mumbai Indians and Chennai Super Kings, given when Mumbai Indians lost their wickets, their expected score was 146. They ended up with 162/9. In response, the effective chase for Chennai Super Kings was 179 as shown in the chart below.

On April 13, 2014, Chennai Super Kings beat Kolkata Knight Riders by 9 wickets, in a chase of 140. They reached 143/1 in 81 balls. Their effective target in that game was 67.9 runs. In the 2019 IPL final, Mumbai Indians expected score batting first was 147.2, and they managed 149. They won by 1 run, but Chennai Super Kings made their effective target to be 180.9. That’s the extent to which they fell behind.

I’ll try and post these for as many matches as I can during this IPL. Comments are welcome as usual. I will try to reply to substantive comments.